[ML/DL Attention] argmax vs. softargmax 너무 대충 알고 있던 그것 | (ft. hardmax / softmax)
1. Hard-attention (with argmax)
2. Soft-attention (with softargmax)
--------------------------------------------------------------------------------------
Transformer 를 이해하기 전에 Attention 에 대한 개념을 알아야 한다. Attention 을 위한 Score vector 를 어떤걸로 사용하느냐에 따라 다음 두 가지로 나뉜다 :
1. Hard-attention
2. Soft-attention
이 둘의 차이는 Score vector를 생성할 때 argmax 를 사용하는지 아니면 softargmax 를 사용하는지에 차이다. 그리고 다시 다음과 같은 연쇄적인 적용 관계를 가진다:
- hardmax → argmax → hard-attention
- softmax → softargmax → soft-attention
엥??? 뭔가 헷갈린다. 보통 Neural networks 를 이용한 classifier 의 경우 Softmax + argmax 조합을 사용한다. 즉, Softmax 를 통해 정규화된(normalized)된 모델 스코어에서 가장 큰 값을 가지는 노드의 인덱스를 출력하는게 보통의 classification pipeline 이다.
그런데 위의 관계도는 내가 기존에 알고 있던 조합과 달라서 혼란스러웠다. 그래서 정리했다.
Softmax vs. Hardmax
그리고
Argmax vs. Softargmax
--------------------------------------------------------------------------------------
※ A라는 대상을 바로 이해하기 힘들다면 그와 반대되는 B에 대해서 먼저 이해하라.
>> A : B = Softmax : Hardmax 혹은 Softargmax : Argmax
사실 Hardmax 는 단순히 숫자 리스트에서 최대값을 찾는 것과 같다. 코딩을 한다면 max() 함수를 사용하면 된다. max 함수를 구현한다면 다음과 같이 리스트 순회를 통해 비교하면서 최대값을 구할 수 있다:
data = [3, 1, 2, 5, 6] max_val = None for i in data: if max_val == None or i > max_val: max_val = i print(f"max value: {max_val}")
이렇듯 Hardmax() 함수는 단순히 크기 비교를 통해 가장 큰 값을 반환하는 함수다.
그렇다면 Softmax() 함수는?
Softmax() 함수
이를 한 마디로 정리하면:
- 값 리스트를 exponential function을 통한 표준화된 비율로 정규화(normalized) 시켜서 가장 큰 값에서 비율이 증폭되는 함수.
Hardmax() 함수가 최대값만 짚어내는 impluse function 이라면, Softmax() 함수는 최대값에서 비율 수치가 증폭되는 조금더 스무딩(smoothing)된 형태라고 할 수 있다. 무슨 말인지 다음 예시를 보자.
Softmax Fuction 은 다음과 같이 정의된다:
이를 기반으로 다음과 같은 value table 이 있다고 하자:
- 노란색 영역이 입력 리스트이다
- 입력에 softmax function 정의식을 적용하면 오른쪽과 같은 그래프가 그려진다
- 보는 것 처럼 최대값 8 에서 softmax() 의 반환 값이 가장 높은 비율을 차지한다.
- 즉, 최대값 근처에서 거의 대부분의 확률을 가져간다 = 최대값이 8이 될 확률이 가장 높다
이번에는 입력 범위를 음수 영역까지 포함해서 테스트 해보자:
 |
| input = [-4, 4] 사이의 정수 |
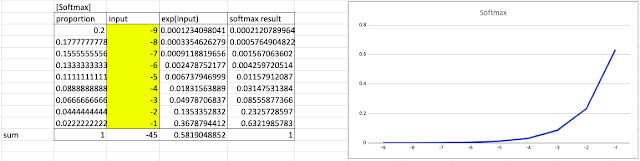 |
| input = [-9, -1] 사이의 정수 |
값의 범위가 바뀌어도 여전히 최대값(maximum value) 에서 가장 높은 비율 값을 반환한다.
- (i.e) Softmax() 함수는 항상 최대값에 sensitive 하다
이 원리를 바탕으로 Softargmax() 가 구현된다.
Softargmax() 함수
한마디로:
softmax() 를 통해 최대값의 인덱스(index)를 근사치(approximate value)로 반환하는 함수다. 근사치이기 때문에 실수값을 반환한다.
- argmax() 는 최대가 되는 위치의 특정 인덱스를 정수값으로 반환한다.
- 이것이 이 둘의 가장 큰 차이점이다.
먼저 Softargmax() 의 정의식은 다음과 같이 유도된다:
 |
| softmax() 를 통해 인덱스 I 의 기대값을 구함 = softargmax() |
즉, Softargmax() := softmax() 확률 값을 통한 인덱스의 기대값 으로 정의된다.
이때, 기본적인 softmax() 함수로 기대값을 구하면 여러 개의 최빈수(mode)가 존재할 때 증폭이 약해지는 성질을 띤다. 최대값은 올리고, 다른 값들은 낮추기 위해 큰 베타(𝛽) 라는 상수 값을 입력 x에 곱한다.
구현
softmax() 함수는 벡터로 표현된다. 그리고 softargmax() 는 softmax() 에 의한 벡터 곱으로 표현할 수 있다.
이러한 계산 방식을 일반화 시키기 위해 argmax 를 구할 때에도 hardmax() 함수가 벡터를 반환시킬 필요가 있다.
이때 hardmax() 함수는 다음과 같이 다시 정의할 수 있다:
- a hard version of softmax which returns 1 for the maximum component and 0 for all the others
- 즉, 최대값의 위치를 나타내는 one-hot 벡터이다
구현은 다음과 같다:
- 주어진 데이터의 최대값은 2.1 이다
- hardmax() 벡터를 통해 argmax() 를 구하면 정확히 최대값 2.1 이 위치하는 인덱스 3을 반환한다
- softmax() 를 통한 기대값 인덱스는 2.56 이다
- 베타 상수를 곱한 향상된 softmax() 를 사용하면 기대값 인덱스는 2.999 (= softargmax)
- 즉, softargmax() 는 argmax() 를 근사화 시킨 함수로 볼 수 있다
[정리]
- argmax : hardmax 를 이용한 최대값의 인덱스 구하기
- softargmax : softmax 를 활용한 근사된 최대값의 인덱스 구하기
Softargmax() 를 사용하는 이유
- argmax() 는 미분이 불가능하다 (impulse 함수)
- 미분이 불가능하면 기울기 기반의 최적화 알고리즘을 사용할 수 없다 (= 딥러닝 학습 X)
- 따라서, 미분이 가능한 형태의 argmax() 함수가 필요하다
- 그 대안으로 Softargmax() 가 사용된다.
Softargmax() 의 활용 예시는 (ref5)를 참고하자.
※ colab 구현
위의 코드를 실행하면 다음을 알 수 있다:
- beta 항이 곱해진 향상된 Softmax 신호가 Hardmax의 one-hot 시그널과 유사해진다
- 그러면서도 미분이 가능한 형태다
즉, beta-softmax는 hardmax의 명확성과 softmax의 미분가능성을 모두 가진 형태로 생각할 수 있다
--------------------------------------------------------------------------------------
Reference
개념 관련
1. https://bouthilx.wordpress.com/2013/04/21/a-soft-argmax/
2. https://www.tutorialexample.com/understand-softargmax-an-improvement-of-argmax-tensorflow-tutorial/
3. https://stats.stackexchange.com/questions/298849/soft-version-of-the-maximum-function / 어떻게 벡터로 표현하지?
4. https://m.blog.naver.com/sw4r/221378182223
5. https://powerofsummary.tistory.com/154
구현 관련
6. https://medium.com/@nicolas.ugrinovic.k/soft-argmax-soft-argmin-and-other-soft-stuff-7f94e6120dff
7. https://titanwolf.org/Network/Articles/Article?AID=f2607f6e-78e3-4916-9f3c-c1ff65b8c941
기타
8. https://www.youtube.com/watch?v=KpKog-L9veg / 영상자료
9. https://www.youtube.com/watch?v=M59JElEPgIg / 미분가능 함수
10. https://www.youtube.com/watch?v=ytbYRIN0N4g / 심도 있게 이해하기
11. https://www.youtube.com/watch?v=Z3qBybK4bZg / Softmax 라고 부르는 이유에 대한 설명
12. https://atcold.github.io/pytorch-Deep-Learning/en/week12/12-3/ / NYU-DLSP20





댓글
댓글 쓰기